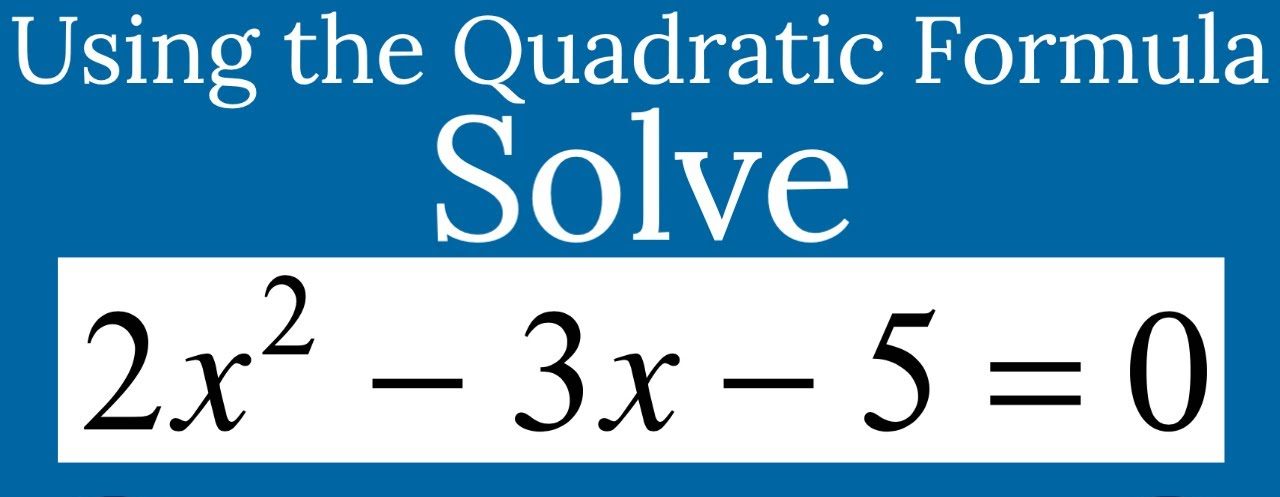Mathematics is a universe of numbers and equations, each holding its unique challenge and intrigue. Among these, quadratic equations stand out as both fundamental and fascinating. In this article, we delve into the world of quadratics through the lens of one specific equation: 2×2-3x- 5 = 0. This equation may seem daunting at first glance, but it opens a door to a deeper understanding of algebraic concepts and problem-solving techniques.
Whether you are a student grappling with algebra, a math enthusiast, or just someone curious about how these equations work, this guide is tailored for you. We will journey through various methods of solving this equation, including factoring, using the quadratic formula, and completing the square. Along the way, we’ll uncover the beauty and logic embedded in the algebraic structure, offering insights that go beyond just finding the solution.
By the end of this article, you will not only have mastered the techniques to solve 2×2-3x- 5 = 0 but also gained a deeper appreciation for the elegance and power of mathematics. So, let’s dive into this mathematical adventure and unlock the secrets of quadratic equations together!
Understanding the Equation 2×2-3x- 5 = 0
Before diving into solving the equation 2×2-3x- 5 = 0, it’s crucial to understand its components. This equation is a classic example of a quadratic equation, which is any equation that can be rearranged into the standard form ax^2 + bx + c = 0, where a, b, and c are constants, and x represents an unknown variable.
In our equation:
- a (the coefficient of x^2) is 2,
- b (the coefficient of x) is -3, and
- c (the constant term) is -5.
Quadratic equations are notable for their curved graphs, known as parabolas, and they typically have two solutions. These solutions can be real or complex numbers, and they represent the points where the parabola intersects the x-axis.
Methods of Solving Quadratic Equations
There are several methods to solve quadratic equations like 2×2-3x- 5 = 0. Let’s explore three common methods:
1. Factoring
- This involves rewriting the quadratic as a product of two binomials.
- For 2×2-3x- 5 = 0, factoring can be tricky as it does not factor neatly. We would need to find two numbers that multiply to 2*(-5) = -10 and add up to -3, which is not possible in this case.
2. Quadratic Formula
- A more universal method, it uses the formula: x = [-b ± √(b^2 – 4ac)] / 2a.
- Applying this to our equation gives two solutions, which are the roots of the equation.
3. Completing the Square
- This method involves rearranging the equation into a perfect square plus a constant.
- It’s a bit more complex but offers a deeper understanding of how quadratics work.
Graphical Interpretation
Graphically, a quadratic equation forms a parabola. For 2×2-3x- 5 = 0:

- The parabola opens upwards (since the coefficient of x^2 is positive).
- The vertex of the parabola provides the equation’s minimum value.
- The x-intercepts (if they exist) are the solutions of the equation.
Using graphing software or manual plotting, one can visualize how the solutions relate to the graph of the equation.
Real-world Applications
Quadratic equations are more than just academic exercises. They have practical applications in various fields:
- Physics: Projectile motion equations are quadratics.
- Engineering: Parabolic shapes are used in designing bridges and antennas.
- Economics: Quadratics can model cost and revenue functions.
Understanding these equations can provide insights into complex real-world problems.
Common Mistakes and Tips
Common mistakes while solving quadratics include:
- Misapplying the formula: Ensure all terms are on one side of the equation.
- Arithmetic errors: Particularly in the quadratic formula.
Tips for success:
- Double-check your work: Especially the discriminant (b^2 – 4ac) in the quadratic formula.
- Practice with different methods: This builds a deeper understanding.
Conclusion:
In this journey through the realms of algebra, we have untangled the complexities of the quadratic equation 2×2-3x- 5 = 0, exploring various methods to find its solutions. From the straightforward yet sometimes intricate process of factoring to the universally applicable quadratic formula, and the insightful method of completing the square, we have seen how each technique offers its unique perspective in solving quadratic equations.
Through graphical interpretation, we visualized how these abstract numbers and variables paint a concrete picture on a graph, enhancing our understanding of the equation’s behavior. Moreover, by discussing real-world applications, we bridged the gap between theoretical mathematics and practical scenarios, showcasing the relevance and importance of quadratic equations in various fields.
However, as with any mathematical endeavor, the journey is fraught with potential pitfalls. Common mistakes can easily derail our problem-solving process. Yet, with practice and careful attention to detail, these obstacles become stepping stones to mastery. The tips provided aim to guide you in avoiding these errors and in refining your problem-solving skills.
As we conclude, remember that mathematics is not just about finding the right answers; it’s about understanding the ‘why’ and ‘how’ behind those answers. Equations like 2×2-3x- 5 = 0 are not just problems to be solved but opportunities to deepen our analytical thinking and appreciate the beauty and logic of mathematics. So, keep exploring, and keep questions.